数据结构三

 左偏树可能各个方面都是最优的，可能他的最大缺点是插入操作O(n)，但是综合并操作与代码难度考虑还是不错的选择

至于他的已知节点删除和变种没实现，待以后用的话再补上吧，觉得几乎没用处？（不敢说XD...

 

/****************************************
*                 LeftHeap.h
*		Describe: 可并优先队列——左偏树
*       Created: 2010-5-27
*       CopyRight  2010,Leek
*
******************************************/
#include <iostream>
#include <vector>
#include <queue>
using namespace std;

typedef int Type;

typedef struct LNode
{
	Type key;
	int dis;
	LNode *left;
	LNode *right;
	LNode (Type key)
	{
		dis = 0;
		left = NULL;
		right = NULL;
		this->key = key;
	}
}LNode;
typedef LNode *PLNode;


void Swap (int &a, int &b)
{
	a ^= b, b ^= a, a ^= b;
}


void Swap (PLNode &a, PLNode &b)
{
	PLNode tmp = a;
	a = b, b = tmp;
}




PLNode LHeap_Merge (PLNode a,PLNode b)
{
	if (a == NULL)
		return b;
	if (b == NULL)
		return a;
	if (a->key > b->key)
		Swap (a->key,b->key);
	a->right = LHeap_Merge (a->right, b);
	if (a->left == NULL || a->right->dis > a->left->dis)
		Swap (a->right,a->left);
	if (a->right == NULL)
		a->dis = 0;
	else
		a->dis = a->right->dis + 1;
	return a;
}

PLNode LHeap_Build (queue<PLNode> &a)
{
	PLNode tmp = a.front();
	while (a.size() > 1)
	{
		a.pop();
		tmp = LHeap_Merge (tmp,a.front());
		a.push(tmp);
		a.pop();
		tmp = a.front();
	}
	return a.front();
}


PLNode LHeap_Insert (Type key,PLNode root)
{
	PLNode tmp = new LNode(key);
	return LHeap_Merge (tmp,root);
}

Type LHeap_Delete_Min (PLNode &root)
{
	PLNode tmp = root;
	root = LHeap_Merge (root->left, root->right);
	Type top = tmp->key;
	delete tmp;
	return top;
}

 

觉得建树和并操作值得思考多少有点启发性吧

顺便贴上败者树的模板  今天复习结束看漫画去

 

/****************************************
*                 Loser.h
*		Describe: 败者树
*       Created: 2010-5-27
*       CopyRight  2010,Leek
*
******************************************/
#include <iostream>
using namespace std;

const int N = 1 << 16; //N大于n，并为2的次方
const int n = 234;
typedef int Type;
Type f[N * 2];
Type a[n];
void BuildTree (int n, int f[2 * N])
//建树a存在f N-N+n
{
	memcpy (f + N,a,sizeof (a[0]) *n);
	for (int i = N,j = N + n - 1; i > 1;i >>= 1,j >>= 1)
	{
		for (int k = i; k < j;k += 2)
			f[k >> 1] = f[k] > f[k + 1] ? f[k] : f[k + 1];
		//求得是最大值，可改为最小值
		if (!(j&1))
			f[j >> 1] = f[j];
	}
}

int findmax (int s, int t)
//查询s t中的最大  最小值 
{
	int r = f[s] >= f[t]? s: t;
	for (int i = s,j = t; i < j; i >>= 1, j >>= 1)
	{
		if (!(i & 1) && i + 1 < j && f[i + 1] > f[r])
			r = i + 1;
		if ((j & 1) && j - 1 > i && f[j - 1] > f[r])
			r = j - 1;
	}
	return f[r];
	//以下程序可求a【s t】最大最小值的下标
	while (r < N)
		if (f[r] == f[r << 1])
			r <<= 1;
		else
			if (f[r] == f[(r << 1) + 1])
				r = (r << 1) + 1;
}

 

 

【C/C++】 Coding 数据结构 堆 Comments(96) 2010年5月28日 02:13

数据结构二

 关于平衡二叉树只会AVL和傻X树：（   由于AVL各方面都不如SBT  所以只整理SBT算了。

        但是杯具的是把以前整理写的代码等Ctrl+A Shift+Delete了...

 

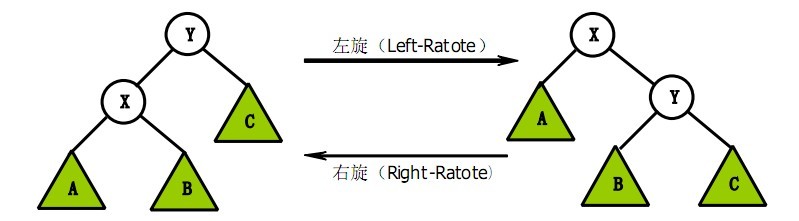
这个是模仿别人的重新写一个，其中删除是最有技巧结合平衡操作很精妙

 

/****************************************
*                 SBT.h
*		Describe: SBT平衡二叉树
*       Created: 2010-5-26
*       CopyRight  2010,Leek
*
******************************************/

#include <iostream>

using namespace std;

typedef int Type;

//	SBT存储结构
class SBTNode
{
public:
	SBTNode *child[2];
	SBTNode *parent;
	Type key;
	int size;
	SBTNode (Type key,int size);
};

typedef SBTNode *SBTree;

enum {Left,Right=1};

SBTNode::SBTNode (Type key,int size)
{
	this->key = key;
	this->size = size;
	child[Left] = child[Right] = parent = NULL;
}

void SBT_Rotate (SBTree &root, bool num)
{
	//num == Left 右旋num == Right左旋
	SBTNode *tmp = root->child[!num];
	tmp->parent = root->parent;
	if (tmp->child[num] != NULL)
		tmp->child[num]->parent = root;
	root->child[!num] = tmp->child[num];
	tmp->child[num] = root;

	tmp->size = root->size;
	root->size = root->child[Left]->size + root->child[Right]->size + Right;
	root = tmp;
}

void SBT_Maintain (SBTree &root, bool num)
{
	//人字型数据退化，但是其他数据速度都快
	if (root->child[num]->child[num]->size > root->child[!num]->size)
		SBT_Rotate (root, !num);
}

void SBT_Insert (SBTree &root, SBTNode *x)
{
	if (root == NULL)
		root = x;
	else
	{
		root->size++;
		x->parent = root;
		SBT_Insert (root->child[x->key > root->key], x);
		SBT_Maintain (root, x->key > root->key);
	}
}

SBTNode *SBT_Search (SBTree &root,Type key)
{
	return root == NULL || root->key == key? root: SBT_Search (root->child[key > root->key], key);
}

SBTNode *SBT_Delete (SBTree &root, Type key)
{
	if (root == NULL)
		return NULL;
	root->size--;
	if (root->key == key || root->child[key > root->key] == NULL)
	{
		SBTNode *tmp;
		if (root->child[Left] == NULL || root->child[Right] ==NULL)
		{
			tmp = root;
			root = root->child[root->child[Left] == NULL];
			if (root != NULL)
				root->parent = tmp->parent;
		}
		else
		{
			tmp = SBT_Delete (root->child[Right], key - Right);
			root->key = tmp->key;
		}
		return tmp;
	}
	else
		return SBT_Delete (root->child[key > root->key], key);
}

SBTNode *SBT_Pred(SBTree root, Type key)
{
    if (root == NULL)
		return NULL;
    if(key <= root->key)
		return SBT_Pred(root->child[Left],key);
    else
	{
        SBTNode *tmp=SBT_Pred(root->child[Right],key);
        return tmp != NULL?tmp:root;
    }
}

SBTNode *SBT_Succ (SBTree &root,Type key)
{
	if (root == NULL)
		return NULL;
	if (key >= root->key)
		return SBT_Succ(root->child[Right],key);
	SBTNode *tmp = SBT_Succ(root->child[Left], key);
	return tmp != NULL? tmp:root;
}

SBTNode *SBT_Select(SBTree root, int i)
{
    int r = root->child[Left]->size+Right;
    if (i == r)
		return root;
    else
		return SBT_Select(root->child[i>r],i>r?i-r:i);
}

int SBT_Rank(SBTree root, Type key)
{
    if (root == NULL)
		return Left;
    if (root->key == key)
		return root->child[Left]->size+Right;
    else
		if(key < root->key) 
			return SBT_Rank(root->child[Left],key);
    else
	{
        int r = SBT_Rank(root->child[Right],key);
        return r == Left? Left: r + root->child[Left]->size + Right;
    }
}

 

 

等有时间改成模板实现吧

 

【算法学习】 Coding 数据结构 Comments(9) 2010年5月27日 00:44

第一次应聘实习 | 排列与阶乘进制

昨天去ND面试 （车上收到有道短信 说下午视频答疑,估计也没什么问题问的就算了 .主考官直接问我什么时候有时间过去 （囧。然后说暑假吧，直接被他否决了 ，说是不能那么晚，现在就得去，平时没时间可以请假一个星期有到三四天就行了...就这样默默地答应了。之后回来打电话给我说明天要过去签协议，补贴方面800保障，出勤好的话每个月加80（可是网上说是1100，这里怎么变了呢 ，他解释什么税收管理费等（= =不是2k以上才要税收吗，显然地有猫腻...被人坑的感觉自然不爽加上路途漫漫（温泉路口 所以今天一大早打电话过去说不去了 酱紫第一次很山寨的笔试面试经历结束了...

        回来继续复习和整理算法。发现模板的《排列与阶乘进制》有猫腻，大牛的代码写的很玄乎看不出是不是真的错了（代码不能多几个注释嘛，然后按自己的想法改动了跑了一下果然假想没错

        现在就说说Coding吧，之前排列与顺序等问题直接都是土土地写地，看了阶乘进制赞叹Knuth大师的伟大（...  然后再看逆过程无比纠结（反正死活看不懂喽，然后偷偷暗想他Coding有问题吧，越看越有问题（= = 鄙视一下自己，经过简单数据验证还好真的是模板的问题（XD

        原先的逆过程：

 

void back(__int64 perm)
{
	int i, j, k, p[N + 1] = {0},mark[N + 1] = {0};
	i = 1;
	while (perm)
	{
		p[i] = perm % (i + 1);
		perm /= ++i;
	}

	for (i = n-1; i >= 1; --i)
	{
		j = n,k = 0;
		while (k <= p[i])
		{
			if (!mark[j++])
				k++;
		}
		j++;
		a[j] = i + 1;
		mark[j] = 1;
	}
	j = 1;
	while (mark[j])
		j++;
	a[j] = 1;
}
修改后代码：
void back(__int64 perm)
{
	int i, j, k, p[N + 1] = {0},mark[N + 1] = {0};
	i = 1;
	while (perm)
	{
		p[i] = perm % (i + 1);
		perm /= ++i;
	}

	for (i = n-1; i >= 1; --i)
	{
		j = 1,k = 0;
		while (k <= p[i])
		{
			if (!mark[j++])
				k++;
		}
		j--;
		a[n-i] = j;
		mark[j] = 1;
	}
	j = 1;
	while (mark[j])
		j++;
	a[N] = j;
}

顺便贴上转化为阶乘进制代码：
int KnuthPEncode()
{
	int i,j;
	int place = n,e = 0;
	for (i = 1; i <= n; ++i)
	{
		int t = a[i];
		e *= place--;
		for (j = i+1; j <= n ; ++j)
			a[j] < t &&  e++;
	}
	return e;
}

【算法学习】 Coding 数据结构 实习 Comments(21) 2010年5月26日 20:25

数据结构一

 由于应聘网龙实习生耽搁了，先把整理好的基础部分贴出来

        据说ND招实习生就是招廉价劳动力？随便吧，反正不打算能做成怎么样可以向大牛们学点东西才是关键。在想要是实习住宿问题怎么解决？YOYO大人赞助吧？嗯..

        不扯淡了直接晒代码

        

//*************二叉堆相关操作*********************
void Sink（int p）
{
	int q = p << 1, tmp = heap[p];
	while (q <= hs)
	{
		if (q < hs && heap[q + 1] < heap[q])
			++q;
		if (heap[p] < heap[q])
			break;
		heap[q] = heap[p];
		p = q;
		q <<= 1;
	}
	heap[p] = tmp;
}

int Delete_MinI()
{
	int r = heap[1];
	heap[1] = heap[hs--];
	Sink(1);
	return r;
}

int Delete_MinII()
{
	heap[1] ^= heap[hs], heap[hs] ^= heap[1], heap[1] ^= heap[hs--];
	Sink(1);
	return heap[hs + 1];
}

void Swim(int p)
{
	int q = p >> 1, tmp = heap[p];
	while(q && tmp < heap[q])
	{
		heap[p] = heap[q];
		p = q;
		q >>= 1;
	}
	heap[p] = tmp;
}

void Insert(int p)
{
	heap[++hs] = p;
	Swim(hs);
}

void Build()
{
	for (int i = hs / 2; i ; --i)
		Sink(i);
}




/**********并查集************************/

void Make_Set(int x)
{
	rank[x] = 0;
	p[x] = x;
}

int Find_Set(int x)
{
	int px = x, tmp;
	while (px != p[px])
		px = p[px];
	while (x != px)
	{
		tmp = p[x];
		p[x] = px;
		x = tmp;
	}
	return px;
}

void Union_Set(int a,int b)
{
	a = Find_Set(a);
	b = Find_Set(b);
	if (rank[a] < rank[b])
	{
		p[a] = b;
	}
	else
	{
		p[b] = a;
		if (rank[a] == rank[b])
			++rank[a]; 
	}
}



/************哈希表********************/

 //质数1811 5087 10657 50503 100109 500119

int hash[Size * Size][2];
int first[Size][Size];
int next[Size * Size];
int entry = 1;

/*********************/

//      值太大二维存储   ps：从没用过  似乎没必要?

/*********************/
int Insert_Find_Hash()  
{
	long long a, b;
	a = 前半部分的值（可按位存储）;b = 后半部分;
	c = a % Size; d = b % Size;
	e = first[c][d];
	while (e != 0)
	{
		if (hash[e][0] == a && hash[e][1] == b)
			return 0;
		e = next[e];
	}
	hash[entry][0] = a;
	hash[entry][1] = b;
	next[entry] = first[c][d];
	first[c][d] = entry;
	entry ++;
	return 1;
}

bool Insert_Find_Hash(Type x)
{
	unsigned int key;
	key = Hash(x);
	p = first[key];
	while (p)
	{
		if (hash[p] == x)
			return false;
		p = next[p];
	}
	hash[entry] = key;
	next[entry] = first[key];
	first[key] = entry;
	entry ++;
	return true;
}

//字符串用的Hash函数

unsigned int SDBMHash(char *str)
{
	unsigned int hash = 0;
	unsigned int len = 0;
	while (*str)
	{
		// hash = 65599*hash + (*str++);	
		hash = (*str++) + (hash << 6) + (hash << 16) - hash;
		++len;
	}
	hash = (len) + (hash << 6) + (hash << 16) - hash;
	return (hash & 0x7FFFFFFF);
}

/**********Good to the last code************/

        下期：平衡二叉树

【算法学习】 Coding 数据结构 Comments(1) 2010年5月22日 07:42